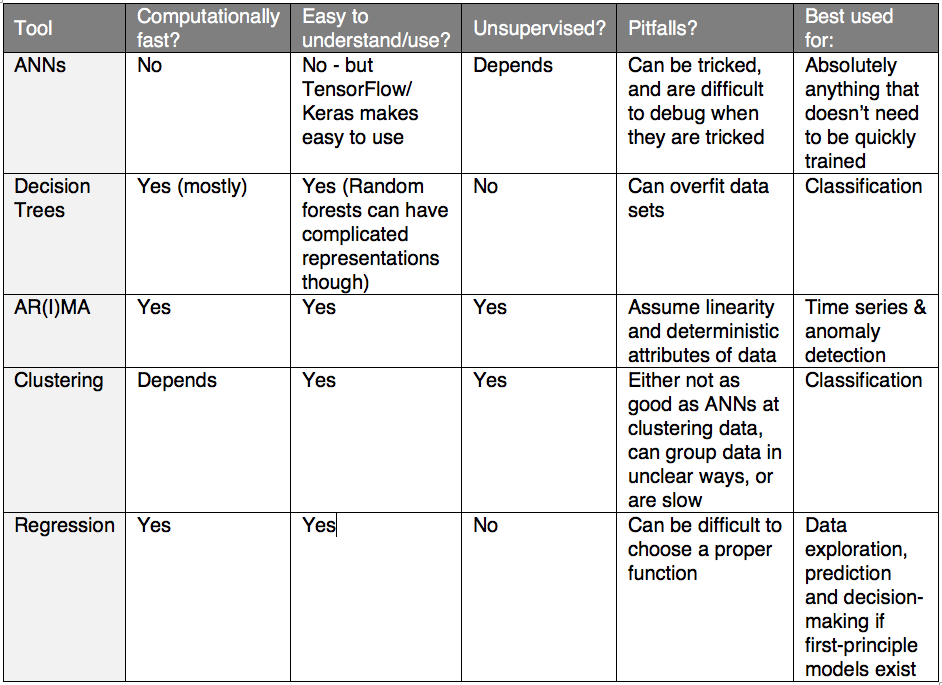
Machine learning’s utility in the commercial landscape has been firmly established, and its popularity is on an accelerated rise, so it’s no wonder there’s a scramble to assemble teams versed in the field. With the multitude of techniques available to tackle problems ranging from predicting user conversion rates, to recognizing images, to automatically generating content, it can be a bit disorienting to determine which ones you or your team should use to meet project demands. Let’s take a moment to examine and compare a few of the popular techniques data scientists employ.
Artificial Neural Networks (ANNs)
By far the hottest topic in the machine learning universe today, and one that merits some description. A set of “neurons” receive some input (the value of some variables), process it (act on the variables with functions), then pass the results onto another set of neurons that continue the input->output chain. At some point, the sequence is terminated, and the results are interpreted, unusually answering the questions “What is it?”, “What’s the value?”, or “What action should be taken?” There are a dizzying number of topologies (ways to feed the outputs of one set of neurons into the next set) and activation functions (the functions that process what the neurons are given) to choose from. The topologies include: feed forward networks (FNNs, which are the most straight-forward to visualize), convolutional neural networks (CNNs, which try to mimic cone cells and the vision processing area of the brain), recursive neural networks (RNNs, which include neurons that talk to themselves), and generative adversarial networks (GANs, which are one of the newest additions to the family, and essentially learn to make new variations of things, like art or language, based on existing versions).
Pros
We can design machine “brains” that are way better at recognizing some patterns than us, and can automate seemingly human processes!
Cons
Extracting first principles from data (i.e. learning by example) is NP-hard (computationally very slow), so, generally, we need to be able to design topologies and choose activation functions that converge on a solution for a specific problem quickly. This is difficult since the bulk of the field is relatively new and still in the heuristic stages of development – we need a stronger math framework. Efforts have been made to train networks that can train other networks, but this goes down the NP-hard rabbit hole, and creating a network that can automate the data scientist’s job would result in an algorithm that is infeasible to run on (clusters of) conventional machines. There are also ways to trick neural networks in the silliest of ways, which are hard to debug when ANNs are often treated as black boxes.
Decision Trees
These are basically flow charts. Decision trees ask a question about a data set at each fork, then split the data into groups based on the answer, and pipe the groups to the next fork. There are a few kinds of decision tree-type algorithms, primarily comprising “random forests” (which divvy a data set up into random smaller sets before training) and C4.5/C5.0 (which attempt to minimize the Shannon entropy – a canonical measure of disorder – of the categorized sets of data).
Pros
Decision trees are very simple to implement, and tend to optimize some well-motivated objective function to solve categorical classification problems.
Cons
Variants that aren’t random forests frequently overfit training data, and are thus hit-or-miss for correctly classifying any future data sets. Meanwhile, random forests are slow and, while they minimize error on future data sets, they might not correctly classify any given data set as well as, e.g. C4.5/5.0.
AR(I)MA
Short for “auto regressive (integrated) moving average.” These models can be extremely useful for answering questions about data that actively streams in time, like network activity or seasonal customer conversation rates, and are especially useful to detect anomalous behaviors. They basically assume the data can be modeled as a linear differential equation of arbitrary order that is subject to noise – something with huge predictive power – and determine what the differential equation actually is.
Pros
AR(I)MA models are simple to implement, and very easy to understand with a little background in differential equations. They’re also an unsupervised way of detecting anomalies, meaning once the algorithm is set up, the data scientist doesn’t need to tell it anything – the data speaks for itself!
Cons
These models assume the response of the system to random events is deterministic, which it isn’t always (people can be random and complicated). Additionally, few things in reality are actually linear.
Clustering
Clustering groups data points into, well, clusters, which are useful for, e.g., identifying types of images or customer behaviors. Two prominent clustering techniques include K-means (which groups data into K different clusters) and hierarchical (which forms clusters by successively grouping groups).
Pros
Clustering provides a method of unsupervised classification, and serves as the progenitor to generative models (e.g. the exciting world of GANs!).
Cons
K-means has difficulty handling groups of data with parameters that don’t naturally group spherically around the average value, while hierarchical is computationally inefficient. The techniques also don’t make sense when classification isn’t well-defined.
Regression
Simply come up with a function that matches the data and, well, fit it to data. You’ll frequently see “linear” appended as a prefix to this, which just fits a line to the points, but, generally, we can fit whatever function makes sense.
Pros
Linear regression is probably the simplest statistical technique that can be applied, and is the easiest for computers to solve. Even using nonlinear models can be very easy to fit with a little bit of linear algebra elbow grease.
Cons
Again, few things in reality are actually linear, so linear regression will usually just be used as a first pass in data exploration to get a sense of trends. Linear combinations of nonlinear functions can overfit data, and determining optimal nonlinear functions is usually best left to neural networks if a first-principle model isn’t discernible.
To summarize concisely: